reveal.js

## Sequence alignments
![dna](images/alignments/title_slide.png)             
              
---

## Assignment

* https://github.com/cphg/sequence_alignment
* Implement local alignment of two sequences that can use affine gap penalties
* Skeleton code is provided in python
* Simple test cases are also provided  
* Clone the repo, implement the `smith_waterman` function in `align_sequences.py`
* You can test your work by running `python3 testdriver`

---

## Local alignment (Smith-Waterman algorithm) 
**Initialization:** $F(i,0) = F(0,j) = 0$

**Iteration:**

`$$F(i,j) = max \left\{
                \begin{array}{1}
                  0\\
                  F(i-1,j) - gap\\
                  F(i-1, j-1) + score\\
                  F(i, j-1) -gap
                \end{array}
              \right\} $$`

**Termination:** Anywhere

---

## Local alignment (Smith-Waterman algorithm with affine gap)

$$S = O + k*E$$
* With affine gaps you could:
    * open a gap
    * extend a gap
* So when considering a gap compare
    * cost of opening a new gap
    * cost of extending an already existing gap
* [Smith-Waterman algorithm with pseudocode](https://en.wikipedia.org/wiki/Smith–Waterman_algorithm)

---

## Algorithmic complexity

Measure of how long an algorithm would take to complete given an input of size $n$.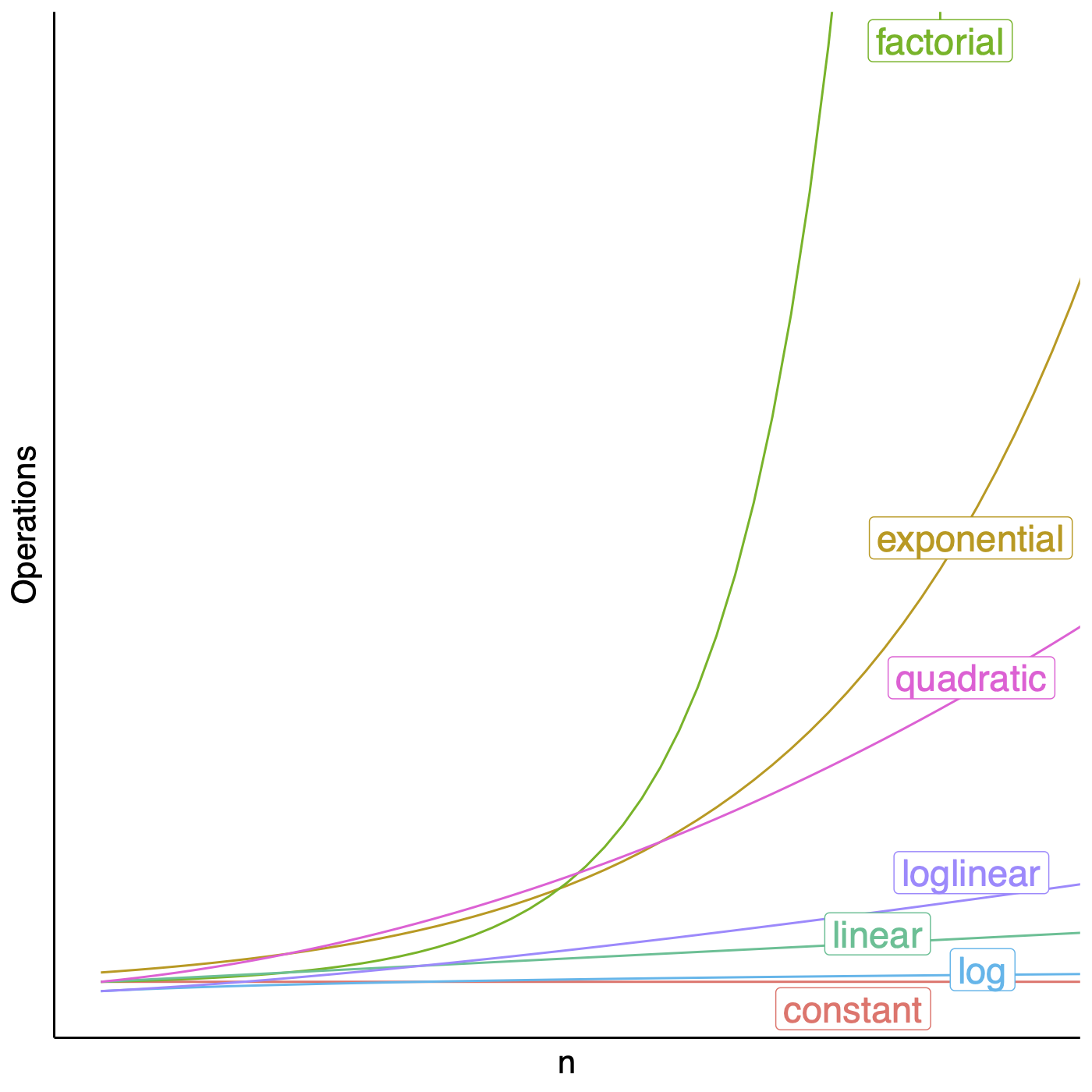

![growth](images/alignments/growth.png)

Note: You can talk about space complexity and/or time complexity. You assume that the underlying factor affecting your program's performance and efficiency is the hardware, OS, and CPU you use. There are also ways of talking about complexity in terms of the average case, best case (though that is never what you should concern yourself with), worst case.

---

## Algorithmic complexity

```python
def is_even_or_odd (n):
    print("Even") if n%2 == 0 else print("Odd")
```

Note: O(1)

---

## Algorithmic complexity

```python
def calcFactorial (n):
  factorial = 1
  for i in range(2,n+1):
    factorial = factorial * i
  return factorial
```

Note: O(n)

---

## Algorithmic complexity

```python
# Binary search, returns index of x in arr if present, else -1
def binary_search(arr, low, high, x):
    if high >= low:
        mid = (high + low) // 2
        if arr[mid] == x:
            return mid
        elif arr[mid] > x:
            return binary_search(arr, low, mid - 1, x)
        else:
            return binary_search(arr, mid + 1, high, x)
    else:
        return -1

# Function call
result = binary_search(arr, 0, len(arr)-1, x)
```

Note: O(log n)

---

## Algorithmic complexity

```python
def fibonacci(n):
  if n==1 or n==0:
    return 1
  return fibonacci(n-1) + fibonacci(n-2)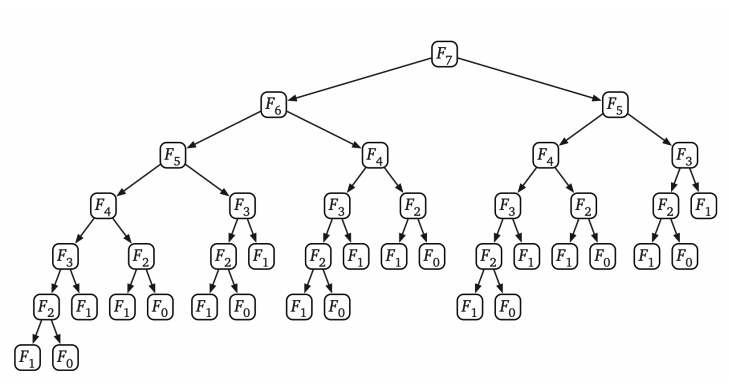
```

![F7](images/alignments/f7.png)

---

## Time Complexity

<section>
<small>
\[\begin{aligned}
T(n) & = T(n-1) + T(n-2) + 1 \\
& < 2 \times T(n-1) + 1 \\
& < 4 \times T(n-2) + 3 \\
&  \ldots \\
& < 2^k \times T(n-k) + (2^k - 1) \\
& = \ldots \\
& < 2^n \times T(0) + (2^n - 1) \\
& = 2^n + 2^n - 1 \\
& = O(2^n)
\end{aligned} \]
</small>
</section>

Note: In reality the time complexity of this recurrence is O(1.618^n)

---

## Computing Fibonacci numbers

```python
def fibonacci(n):
  fib_table = {}
  fib_table[1] = 1
  fib_table[2] = 1
  for i in range(3,n+1):
    fib_table[i] = fib_table[i-1] + fib_table[i-2]
  return fib_table[n]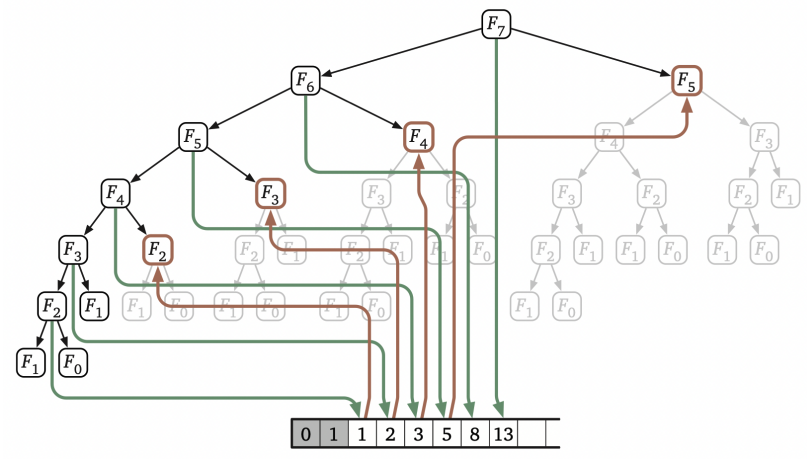
```

![F7](images/alignments/f7_memoize.png)

Note: What is the time complexity here? O(n). This is a dynamic programming algorithm: basically recursion, but with intentional evaluation order, usually filling out a table systematically.

---

## Seed, Anchor, Extend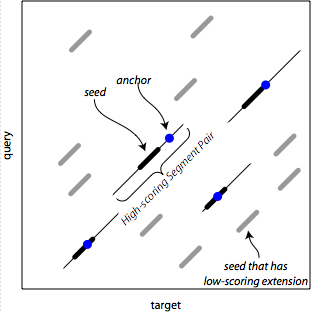

![seeds and HSPs](images/alignments/seeds_and_hsps.png)

<small>Source: [LASTZ documentation](https://www.bx.psu.edu/~rsharris/lastz/README.lastz-1.04.15.html)</small>

Note: middle of the highest-scoring 31-bp interval in the HSP

---

## Seed, Anchor, Extend

![ydrop](images/alignments/ydrop.png)

<small>Source: [LASTZ documentation](https://www.bx.psu.edu/~rsharris/lastz/README.lastz-1.04.15.html)</small>

---

## BWA for alignments

![BWA help](images/alignments/bwa_help.png)

---

## Reproducible alignments

What could cause differences in alignments in different runs of the same set of reads?

[On genomic repeats and reproducibility](https://academic.oup.com/bioinformatics/article/32/15/2243/1743552)

Note: Equally likely alignments, one is selected at random; difference in number of threads used can cause differences in number of reads used to determine mean and sd of fragment length.

---

## Each read is aligned independently
![alignment](images/alignments/realignment.png)

---

## Be careful in regions that are different
![alignment](images/alignments/sv.png)

---

## Mind the gap
![alignment](images/alignments/telomere.png)

---

## SAM format

```shell
samtools flagstats 1474_TNMatch_T.sorted.bam
```

```text
103179474 + 0 in total (QC-passed reads + QC-failed reads)
103179474 + 0 primary
0 + 0 secondary
0 + 0 supplementary
30618344 + 0 duplicates
30618344 + 0 primary duplicates
91410312 + 0 mapped (88.59% : N/A)
91410312 + 0 primary mapped (88.59% : N/A)
103179474 + 0 paired in sequencing
51589737 + 0 read1
51589737 + 0 read2
90175864 + 0 properly paired (87.40% : N/A)
90287592 + 0 with itself and mate mapped
1122720 + 0 singletons (1.09% : N/A)
4776 + 0 with mate mapped to a different chr
4536 + 0 with mate mapped to a different chr (mapQ>=5)

```

---

## BLAST output

![blast](images/alignments/blast_output.png)

Note: Indicates the number of hits or alignments that are expected to be seen by random chance with the same score or better. The lower the E-value, the more significant the alignment (the closer to 0, the better).

---

## Short-read alignment
* Input
  * Shorter sequences
  * A sequencing run creates large number of reads
  * Enough to cover genome multiple times
* Output
  * Position of each read $r$ of length $m$ in the reference.
* Motivation
  * Resequencing
  * More is better!!

---

## `GATTACA` in the human genome
* Brute-force
  * Scan each *k*-mer in the reference
* Analysis:
  * Genome size: 3,000,000,000
  * Query length:  7
  * Number of comparisons: 21,000,000,000
  * Assuming each comparison takes 1/1,000,000,000 of a second
    * Running time: 0.24 days (for one 7bp read)

Note: And a possible solution is an index
 
---

## Indices
* Considerations
  * Space for the index
  * Time required to build index
  * Time required for searching
* Approaches
  * Hash-table based 
    * BFAST, MAQ, MOSIAK, SHRiMP, SOAP, $\ldots$
  * Suffix-tree or BWT based
    * Bowtie, BWA, SOAP2, $\ldots$

---

## Word position table
* Encoding : A=$00_2$, C=$01_2$, G=$10_2$, T=$11_2$
* Build an inverted index of every *k*-mer in the genome
* `GATTACA` = $10001111000100_2$ = $9156_{10}$

![word](images/alignments/word_position.svg)

---

## Burrows-Wheeler transform
* Initially developed for compression
* Reversible permutation of the characters of a string

![BTW](images/alignments/BWT.png)

---

## Burrows-Wheeler transform
```code
def rotate(sequence, n):
    return sequence[n:] + sequence[:n]

def BWT(sequence):
    seq = sequence + "$" 
    perms = [rotate(seq,i) for i in range(len(seq))] 
    return "".join([x[-1] for x in sorted(perms)])
```

```text
>>> string = "abaaba"
>>> BWT(string)
'abba$aa'

>>> string = "Let_me_tell_you_a_little_story_all_about_the_DNA"
>>> BWT(string)
'AN_$Deulyateetl___ahlmtLtlllt_ae_tybo_eu__tsioor_'
```

---

## Insight: BWT provides "structure"
$BWT(T)$ orders the characters of $T$ according to alphabetical order of their right context (characters that come after it)

![BWT_insight](images/alignments/BWT_insight.png)

---

## Reversing the BWT

![reversing](images/alignments/BWT_reversing.png)

---

## Reversing the BWT
![reversing](images/alignments/inverting1.svg)
$T=abaaba$

---

## Reversing the BWT
![reversing](images/alignments/inverting2.svg)
$T=abaaba$

---

## Reversing the BWT
![reversing](images/alignments/inverting3.svg)
$T=abaaba$

---

## Reversing the BWT
![reversing](images/alignments/inverting4.svg)
$T=abaaba$

---

## Reversing the BWT
![reversing](images/alignments/inverting5.svg)
$T=abaaba$

---

## Reversing the BWT
![reversing](images/alignments/inverting6.svg)
$T=abaaba$

---

## Reversing the BWT
```code
def invert_BWT(bw):
    '''Given BWT(T) return T.'''
    table = [""] * len(bw) 
    for i in range(len(bw)):
        table = sorted(bw[i] + table[i] for i in range(len(bw)))
    s = [x for x in table if x[-1] == '$']
    assert len(s) == 1
    return s[0][:-1]
```

```text
>>> bw = "abba$aa"
>>> invert_BWT(bw)
'abaaba'

>>> bw = "AN_$Deulyateetl___ahlmtLtlllt_ae_tybo_eu__tsioor_" 
>>> invert_BWT(string)
'Let_me_tell_you_a_little_story_all_about_the_DNA'
```

---

## Insight : LF mapping
* The $i^{th}$ occurrence of $c$ in the last column of the BWM is the same exact
 character as the $i^{th}$ occurrence of $c$ in the first column.

![LF](images/alignments/LF2.png)

---

## FM index
* combining BWT with a few auxilliary data structures
* core of the index is $F$ and $L$ from BWM
* $L$ is the same size as $T$
* $F$ can be represented as an array of $|\sum|$ integers
* $L$ is compressible

---

## More on short-read alignment algorithms

https://cphg.github.io/compgen/slides/short_read.html

---

## Assignment

* https://github.com/cphg/sequence_alignment
* Implement local alignment of two sequences that can use affine gap penalties
* Skeleton code is provided in python
* Simple test cases are also provided
* Clone the repo, implement the `smith_waterman` function in `align_sequences.py`
* You can test your work by running `python3 testdriver`

---