reveal.js

## 
![assemble](images/review1/title.jpg)

---

## Order of growth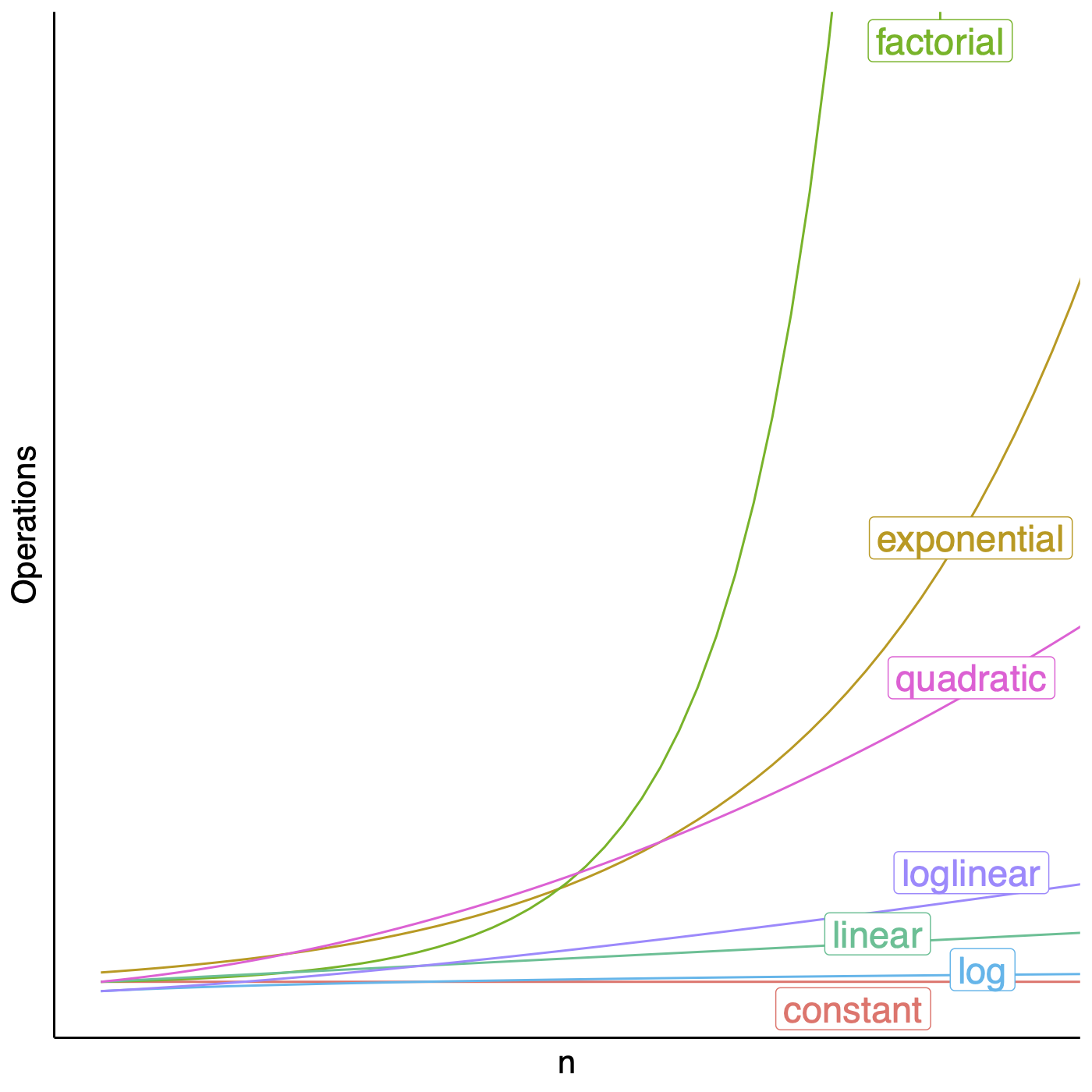

![complexity](images/alignments/growth.png)

Note: Constant runtime is represented by O(1), linear growth is O(n), logarithmic growth is O(log n), log-linear growth is O(n log n), quadratic growth is O(n^2), exponential growth is O(2^n), factorial growth is O(n!).

---

## Algorithmic complexity

```python
def calcFactorial (n):
  factorial = 1
  for i in range(2,n+1):
    factorial = factorial * i
  return factorial
```

Note: O(n)

---

## Algorithmic complexity

```python
def bubble_sort(list_):
    n = len(list_)
    for i in range(n):
        swapped = False
        for j in range(0, n - i - 1):
            if list_[j] > list_[j + 1]:
                list_[j], list_[j + 1] = list_[j + 1], list_[j]
                swapped = True
        # If no two elements were swapped in inner loop, the array is sorted
        if not swapped:
            break
```

```
[5, 1, 4, 2, 8]
```

```
[1, 5, 4, 2, 8]
[1, 4, 5, 2, 8]
[1, 4, 2, 5, 8]
[1, 4, 2, 5, 8]
[1, 4, 2, 5, 8]
[1, 2, 4, 5, 8]
[1, 2, 4, 5, 8]
[1, 2, 4, 5, 8]
```

Note: O(log n)

---

## Algorithmic complexity

```python
# Binary search, returns index of x in arr if present, else -1
def binary_search(arr, low, high, x):
    if high >= low:
        mid = (high + low) // 2
        if arr[mid] == x:
            return mid
        elif arr[mid] > x:
            return binary_search(arr, low, mid - 1, x)
        else:
            return binary_search(arr, mid + 1, high, x)
    else:
        return -1

# Function call
result = binary_search(arr, 0, len(arr)-1, x)
```

Note: O(log n)

---

## Greedy vs. Dynamic Programming

| Feature           | Greedy Algorithm | Dynamic Programming |
|------------------|----------------|---------------------|
| **Definition**   | Makes locally optimal choices at each step. | Break problems into overlapping subproblems and avoid recomputation. |
| **Works on* | *greedy choice property*, *optimal substructure*. | *optimal substructure*, *overlapping subproblems*. |
| **Time Complexity** | O(n) or O(n log n). | O(n²) or O(n³). |
| **Memory Usage** | minimal memory, does not store past results. | Requires additional memory to store subproblem solutions. |

Note: optimal substructure: optimal solution contains within it optimal solutions to subproblems, Greedy-choice property: a globally optimal solution can be arrived at by making locally optimal choices, Overlapping sub-problems: limited number of distinct sub-problems, repeated many times

---

## Coin change

Given a set of coin denominations ${c_1, c_2, ..., c_n}$ and a total amount $S$, find the minimum number of coins needed to make $S$. You can assume you have an infinite number of each coin.

---

## Coin change, Approach 1

1. Always pick the largest coin denomination first.
2. Subtract it from the total amount.
3. Repeat until the total amount becomes zero.

Note:  {1, 3, 4}, S=6, {4, 1, 1}, {3, 3}
```

---

## Coin change, Approach 2

1. Define `N[i]` as the minimum number of coins needed to make amount `i`
2. Use the recurrence

$N[i]=min(N[i−c]+1)$ for all $c$ in coins, if $i−c \geq 0$

---

## Coin change, Approach 2

```python
def dp_coin_change(coins, S):
    N = [float('inf')] * (S + 1)
    N[0] = 0

for i in range(1, S + 1):
        for coin in coins:
            if i - coin >= 0:
                N[i] = min(N[i], N[i - coin] + 1)

return N[S] if N[S] != float('inf') else -1  
```

```
# Example Usage
coins = [1, 3, 4]  # Coin denominations
S = 6  # Target amount
print("Min Coins (DP):", dp_coin_change(coins, S))
```

---

## Coin change, Approach 2

```python
def dp_coin_change_with_coins(coins, S):
    N = [float('inf')] * (S + 1)  # Min coins needed to make amount i
    N[0] = 0  # Base case: 0 coins needed for amount 0
    coin_used = [-1] * (S + 1)  # Track last coin used for each amount

for i in range(1, S + 1):
        for coin in coins:
            if i - coin >= 0 and N[i - coin] + 1 < N[i]:
                N[i] = N[i - coin] + 1
                coin_used[i] = coin  # Store the coin used

# If no solution found, return -1
    if N[S] == float('inf'):
        return -1, []

# Backtrack to find the coins used
    result_coins = []
    amount = S
    while amount > 0:
        coin = coin_used[amount]
        if coin == -1:  # No solution exists
            return -1, []
        result_coins.append(coin)
        amount -= coin  # Reduce amount by selected coin

return N[S], result_coins  # Min coins count and coin combination
```

```
# Example Usage
coins = [1, 3, 4]  # Coin denominations
S = 6  # Target amount
min_coins, used_coins = dp_coin_change_with_coins(coins, S)
print("Min Coins:", min_coins)
print("Coins Used:", used_coins)
```

---

## Gapped Alignment

![matrix](images/alignments/dpmatrix.svg)

---

## Exploring the search space
![matrix](images/alignments/dpmatrix2.svg)

---

## Exploring the search space
![matrix](images/alignments/dpmatrix3.svg)

---

## Seed, Anchor, Extend

![seeds and HSPs](images/alignments/seeds_and_hsps.png)

<small>Source: [LASTZ documentation](https://www.bx.psu.edu/~rsharris/lastz/README.lastz-1.04.15.html)</small>

Note: middle of the highest-scoring 31-bp interval in the HSP

---

## Two approaches to assembly
![intro](images/assembly/alternatives.png)

---