## Hidden Markov Models (HMMs)  Note: HMMs are well-known for their effectiveness in modeling the correlations between adjacent symbols, domains, or events, and they have been extensively used in various fields, especially in speech recognition and digital communication. Considering the remarkable success of HMMs in engineering, it is no surprise that a wide range of problems in biological sequence analysis have also benefited from them. --- ## A toy HMM for 5′ splice site recognition 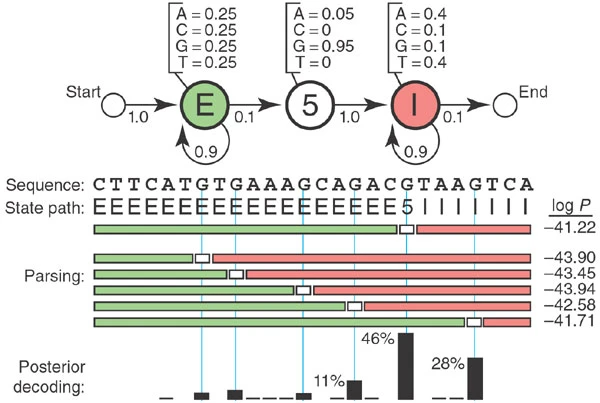 <small>[What is a hidden Markov model?](https://www.nature.com/articles/nbt1004-1315) Note: Often, biological sequence analysis is just a matter of putting the right label on each residue. In gene identification, we want to label nucleotides as exons, introns, or intergenic sequence. In sequence alignment, we want to associate residues in a query sequence with homologous residues in a target database sequence. We can always write an ad hoc program for any given problem, but the same frustrating issues will always recur. One is that we want to incorporate heterogeneous sources of information. A genefinder, for instance, ought to combine splice-site consensus, codon bias, exon/ intron length preferences and open reading frame analysis into one scoring system. How should these parameters be set? How should different kinds of information be weighted? A second issue is to interpret results probabilistically. Finding a best scoring answer is one thing, but what does the score mean, and how confident are we that the best scoring answer is correct? A third issue is extensibility. The moment we perfect our ad hoc genefinder, we wish we had also modeled translational initiation consensus, alternative splicing and a polyadenylation signal. Too often, piling more reality onto a fragile ad hoc program makes it collapse under its own weight. --- ## Local ancestry 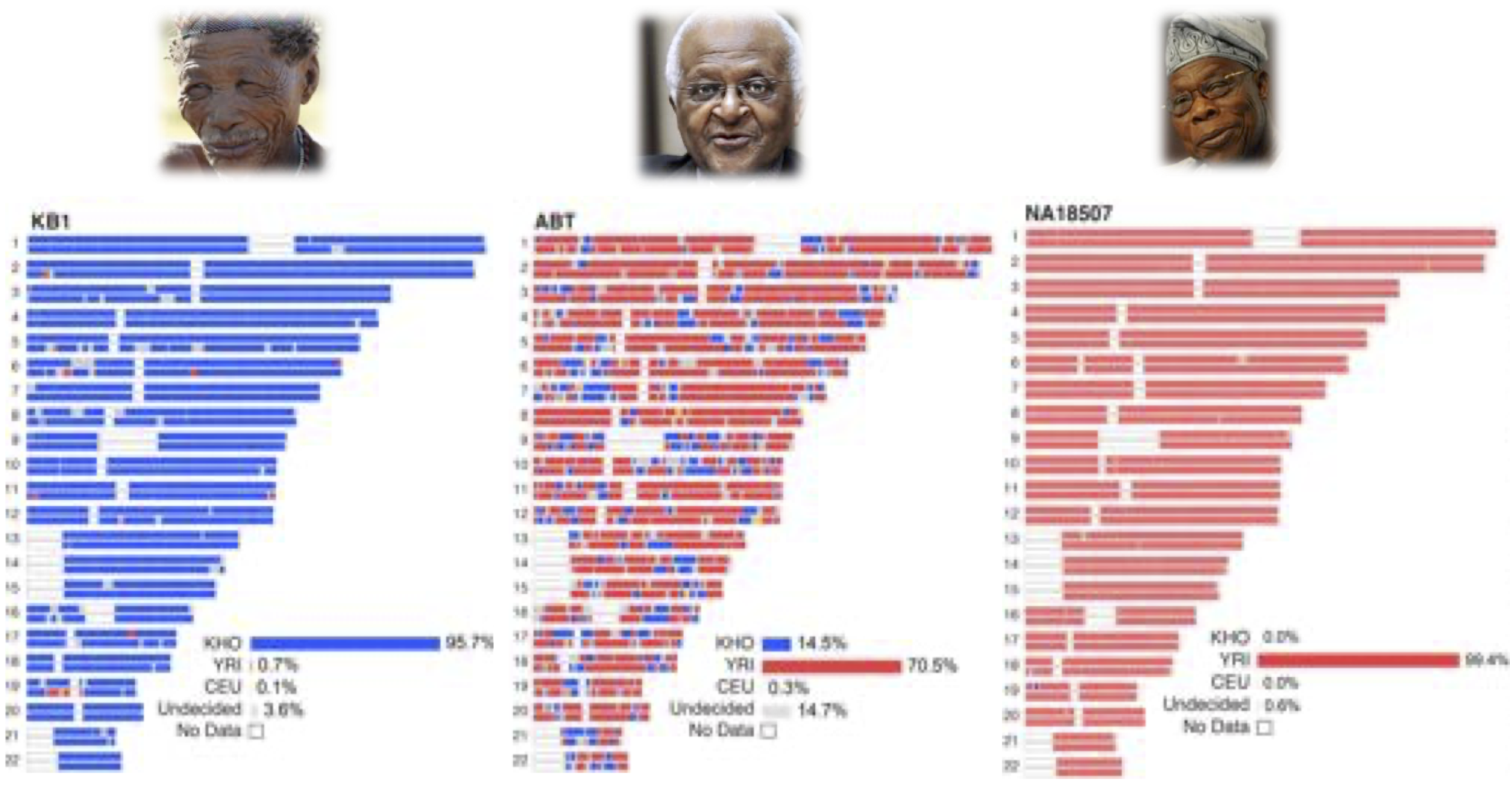 --- ## Hidden Markov Models (HMMs) * Provide a foundation for probabilistic models of linear sequence ‘labeling’ problems * Can be designed just by drawing a graph diagram * The ‘Legos’ of computational sequence analysis * Developed in Electrical Engineering for applications to voice recognition * Gene prediction, protein secondary structure prediction, copy-number variation, chromatin-state assignment, chromatin topology... Note: Joint probability $P(A,B) = P(A|B) P(B) = P(B|A) P(A)$, Marginal probability $P(X=A) = \sum_y P(X=A, Y=y_i)$ --- ## Markov Models * Set of states: ${s_1, s_2, \ldots, s_n}$ * Process moves from one state to another generating a sequence of states: $s_{i1}, s_{i2}, \ldots, s_{ik}, \ldots$ * Markov chain property: $$P(s_{ik}|s_{i1},s_{i2},\ldots,s_{i(k-1)}) = P(s_{ik}|s_{i(k-1)})$$ * The following need to be defined: * transition probabilities $A=(a_{ij}), a_{ij} = P(s_i, s_j)$ * initial probabilities: $\pi=(\pi_i), \pi_i = P(s_i)$ Note: Markov chain property: probability of each subsequent state depends only on what was the previous state --- ## Example  <!-- .element width="80%" height="80%" --> $A = \begin{bmatrix} 0.7 & 0.3\\\\\\ 0.4 & 0.6 \end{bmatrix}$, $\pi = (0.4, 0.6)$ Note: So let's consider I have two coins, one of them is fair and the other one is loaded. --- ## Calculation of sequence probability By Markov chain property, probability of state sequence can be found by the formula $$\begin{eqnarray} P(s_{i1}, \ldots, s_{ik}) &=& P(s_{ik} | s_{i1}, \ldots, s_{i(k-1)}) P(s_{i1}, \ldots, s_{i(k-1)})\\\\\\ &=& P(s_{ik} | s_{i(k-1)}) P(s_{i1}, s_{i2}, \ldots, s_{i(k-1)})\\\\\\ &=& \ldots\\\\\\ &=& P(s_{ik} | s_{i(k-1)}) \ldots P(s_{i2} | s_{i1}) P(s_{i1}) \end{eqnarray}$$ --- ## Calculation of sequence probability  <!-- .element width="80%" height="80%" --> $\pi = (0.4, 0.6)$ Suppose we want to calculate $P(L,L,F,F)$ $$\begin{eqnarray} P(L,L,F,F) &=& P(F|L,L,F) P(L,L,F) \\\\\\ &=& P(F|F) P(F|L,L) P(L,L)\\\\\\ &=& P(F|F) P(F|L) P(L|L) P(L)\\\\\\ &=& 0.7 \times 0.4 \times 0.6 \times 0.6 \end{eqnarray}$$ --- ## Hidden Markov Models * Set of states: ${s_1, s_2, \ldots, s_n}$ * Process moves from one state to another generating a sequence of states: $s_{i1}, s_{i2}, \ldots, s_{ik}, \ldots$ * Markov chain property: $$P(s_{ik}|s_{i1},s_{i2},\ldots,s_{i(k-1)}) = P(s_{ik}|s_{i(k-1)})$$ * States are not visible, but each state randomly generates one of $M$ observations (or visible states): ${v_1, v_2, \ldots, v_M}$ <!-- .element : class="fragment" data-fragment-index="1" --> --- ## Hidden Markov Models * The following need to be defined: * transition probabilities $A=(a_{ij}), a_{ij} = P(s_i, s_j)$ * initial probabilities: $\pi=(\pi_i), \pi_i = P(s_i)$ * observation probabilities: $B=(b_i(v_m)), b_i(v_m) = P(v_m | s_i)$ * Model $M = (A, B, \pi)$ --- ## Example  <!-- .element width="60%" height="60%" --> $A = \begin{bmatrix} 0.7 & 0.3\\\\\\ 0.4 & 0.6 \end{bmatrix}$, $B = \begin{bmatrix} 0.5 & 0.5\\\\\\ 0.3 & 0.7 \end{bmatrix}$, $\pi = (0.4, 0.6)$ --- ## Calculation of sequence probability Suppose we want to calculate $P( \\{ H,H \\} )$ $$\begin{eqnarray} P( \\{ H,H \\} ) &=& P( \\{ H,H \\}, \\{ F,F \\}) + \\\\\\ & & P( \\{ H,H \\}, \\{ F,L \\}) +\\\\\\ & & P( \\{ H,H \\}, \\{ L,F \\}) +\\\\\\ & & P( \\{ H,H \\}, \\{ L,L \\}) \end{eqnarray}$$ $$\begin{eqnarray} P( \\{ H,H \\}, \\{ F,F \\}) &=& P( \\{ H,H \\} | \\{ F,F \\}) P(\\{ F,F \\})\\\\\\ &=& P(H|F) P(H|F) P(F|F) P(F) \end{eqnarray}$$ Note: Consider all possible hidden state sequences --- ## Computational problems with HMMs * Decoding problem : Given the HMM $M=(A,B,\pi)$, and an observation sequence $O$, calculate the most likely sequence of states that produced $O$. * Likelihood problem : Given the HMM $M=(A,B,\pi)$, and an observation sequence $O, o_i \in {v_1,v_2,\ldots,v_M}$, calculate likelihood $P(O|M)$. <!-- .element : class="fragment" data-fragment-index="1" --> * Learning problem : Given observation sequence $O$, and general structure of HMM, determine HMM parameters that best fit the training data. <!-- .element : class="fragment" data-fragment-index="2" --> --- ## Decoding problem Given the HMM $M=(A,B,\pi)$, and an observation sequence $O$, calculate the most likely sequence of states that produced $O$. 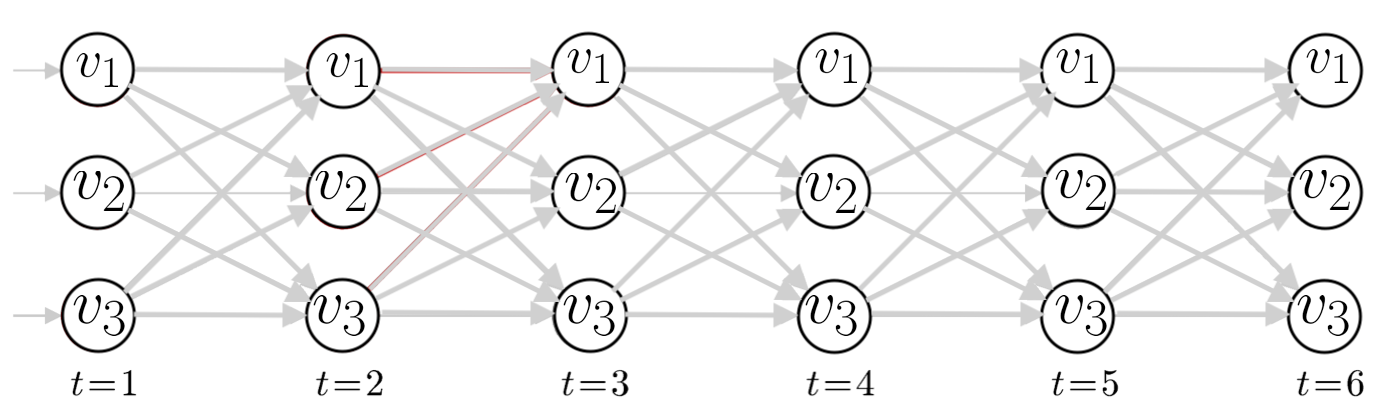 --- ## Decoding problem  $P(O, S)$: the probability that HMM follows sequence of states $S$ and emit string $O$. $$P(O,S) = P(O_{1:T}, S_{1:T}) = P(O_{1:T}|S_{1:T}) P(S_{1:T})$$ $P(O_{1:T}|S_{1:T})$: product of emission probabilities, $P(S_{1:T})$: product of transition probabilities --- ## Decoding problem Find $S_{1:T}$ that maximises $P(O_{1:T}|S_{1:T})$ over all possible paths in the HMM  $M$ states, $T$ time steps: $M^T$ paths... --- ## Viterbi algorithm * Dynamic programming * $M$ rows, $T$ columns * Initialization: $S_{i, 1} = \pi_i B(O_1|S_i)$ * Recursion: $S_{i,j} = \max_k S_{k,j-1} a_{ki} B(O_j|S_i)$  --- ## Viterbi algorithm  <!-- .element width="50%" height="50%" --> Observations : HHTTTTTTTH, $\pi=(0.5,0.5)$ --- ## Viterbi algorithm  <!-- .element width="50%" height="50%" --> Observations : HHTTTTTTTH, $\pi=c(-0.69,-0.69)$  <!-- .element : class="fragment" data-fragment-index="1" --> --- ## Viterbi algorithm  <!-- .element width="50%" height="50%" --> Observations : HHTTTTTTTH, $\pi=c(-0.69,-0.69)$  Note: log(state prior * state emission) -0.69 - 0.69 --- ## Viterbi algorithm  <!-- .element width="50%" height="50%" --> Observations : HHTTTTTTTH, $\pi=c(-0.69,-0.69)$  Note: log(state prior * state emission). -1.2 - 0.69 --- ## Viterbi algorithm  <!-- .element width="50%" height="50%" -->  Note: -1.39 - 0.36 - .69 = -2.44, -1.9 - 0.92 - 0.69 = -3.51 --- ## Viterbi algorithm  <!-- .element width="50%" height="50%" -->  Note: -1.39 - 1.20 - 1.20 = -3.79, -1.9 - 0.51 - 1.20 = -3.60 --- ## Viterbi algorithm  <!-- .element width="50%" height="50%" -->  --- ## Viterbi algorithm  <!-- .element width="50%" height="50%" -->  --- ## Viterbi algorithm  <!-- .element width="50%" height="50%" -->  --- ## Viterbi algorithm  <!-- .element width="50%" height="50%" -->  --- ## Likelihood problem Given the HMM $M=(A,B,\pi)$, and an observation sequence $O$, calculate likelihood $P(O|M)$. $$P(O|S) = \prod_{i=1}^T P(O_i|S_i)$$ But we do not know the state sequence! --- ## Likelihood problem $$\begin{eqnarray} P(O) &=& \sum_{S} P(O,S) \\\\\\ &=& \sum_{S} P(O|S) P(S) \end{eqnarray}$$ Where did we see $P(O,S)$ before? Note: we can compute the total probability of the observations just by summing over all possible hidden state sequences. Again, for M states and T time steps, we are talking M^T paths --- ## Likelihood problem 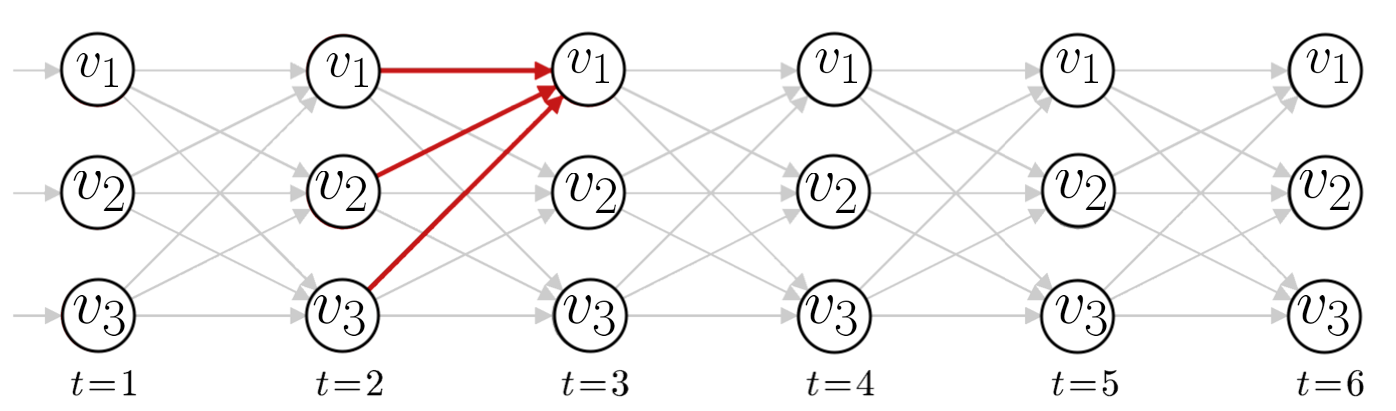 Initialization: $\alpha_1(i) = \pi_i B(O_1|S_i)$ Recursion: $\alpha_{t+1}(i) = \sum_i \alpha_t(i) a_{ij} B(O_{t+1}|S_i)$ $$P(O|M) = \sum_{i=1}^M \alpha_{T}(i)$$ --- ## Likelihood problem  Initialization: $\beta_{T^*}(i) = 1$ Recursion: $\beta_{t}(i) = \sum_j \beta_{t+1}(j) a_{ij} B(O_{t+1}|S_j)$ $$P(O|M) = \sum_{i=1}^M \pi_i B(O_1|S_i) \beta_{T}(i)$$ Note: You can solve the likelihood problem using the forward procedure, or the backwards procedure. --- ## Forward-Backward algorithm $\alpha$ : Probability of the state for observations now and before this time<br> $\beta$ : Probability of the state for observations after this time  Note: Because we are interested in comparison of states at each time point, we have to scale it. So we will calculate alpha-3F * beta3F / sum(alpha_iF*beta_iF). So when using this method, we also get some confidence values associated with our determination of the most likely state --- ## Learning problem Given observation sequence $O$, and general structure of HMM, determine HMM parameters that best fit the training data. * Inputs * $O_1, O_2, \ldots, O_T$ * $v_1, v_2, \ldots, v_M$ * Output * $A$ * $B$ * $\pi$ * Baum-Welch algorithm (EM algorithm) * not guaranteed to be optimal --- ## Estimating parameters for coin flips  --- ## Estimating parameters for coin flips  $P(H|F), P(T|F), P(H|L), P(T|L)$ <!-- .element : class="fragment" data-fragment-index="1" --> $P(F|F), P(F|L), P(L|F), P(L|L)$ <!-- .element : class="fragment" data-fragment-index="2" --> Note: Consider a fully visible Markov model. This would easily allow us to compute the HMM parameters just by maximum likelihood estimation from the training data. For a real HMM, we cannot compute these counts directly from an observation sequence since we don’t know which path of states was taken through the machine for a given input. The Baum-Welch algorithm solves this by iteratively esti- mating the counts. We will start with an estimate for the transition and observation probabilities and then use these estimated probabilities and use the forward-backward procedure to determine the probability of the states at each observation. Then we can use that to determine better estimates of the transition and emission probabilities. --- ## Baum-Welch algorithm $$\hat{a_{ij}} = \frac{\textrm{expected number of transitions from state } i \textrm{ to state }j} {\textrm{expected number of transitions from state }i}$$ $P(S_t = i, S_{t+1} = j, O) = \alpha_t(i)a_{ij}B(O_{t+1}|S_j) \beta_{t+1}(j)$  Note: How do we compute the numerator? Here’s the intuition. Assume we had some estimate of the probability that a given transition i → j was taken at a particular point in time t in the observation sequence. If we knew this probability for each particular time t, we could sum over all times t to estimate the total count for the transition i → j. --- ## Baum-Welch algorithm $$\begin{eqnarray} P(S_t = i, S_{t+1} = j | O) &=& \frac{P(S_t = i, S_{t+1} = j, O)}{P(O)}\\\\\\ &=& \frac{\alpha_t(i)a_{ij}B(O_{t+1}|S_j) \beta_{t+1}(j)}{\sum_{j=1}^N \alpha_t(j) \beta_t(j)} \end{eqnarray}$$ $$\hat{a_{ij}} = \frac{\sum_{t=1}^{T-1} P(S_t = i, S_{t+1} = j | O)}{\sum_{t=1}^{T-1} \sum_{k=1}^M P(S_t = i, S_{t+1} = k | O)}$$ --- ## Baum-Welch algorithm $$\hat{b_j(v_k)} = \frac{\textrm{expected number of times in state } j \textrm{ and observing } v_k} {\textrm{expected number of times in state }j}$$ $P(S_t = j, O) = \alpha_t(j) \beta_t(j)$  --- ## Baum-Welch algorithm $$\begin{eqnarray} P(S_t = j | O) &=& \frac{P(S_t = j, O)}{P(O)}\\\\\\ &=& \frac{\alpha_t(j) \beta_{t}(j)}{\sum_{j=1}^N \alpha_t(j) \beta_t(j)} \end{eqnarray}$$ $$\hat{b_j(v_k)} = \frac{\sum_{t=1\ s.t.\ O_t=v_k}^{T} P(S_t = j | O)}{\sum_{t=1}^{T} P(S_t = j | O)}$$ --- ## Advantages and limitations * Modularity : HMMs can be combined into larger HMMs * Transparency : Based on a state model making it interpretable * Prior knowledge: can be incorporated in the model * Need accurate, applicable, and sufficiently sized training sets of data * Model may not converge to a true optimum * Can be slow in comparison to other methods ---