reveal.js

## Suffix trees, Suffix arrays, Burrows-Wheeler transform
![title](images/short_reads/title.png)

Acknowledgement: Many slides borrowed with permission from Dr. Ben Langmead, JHU

---

## Science update!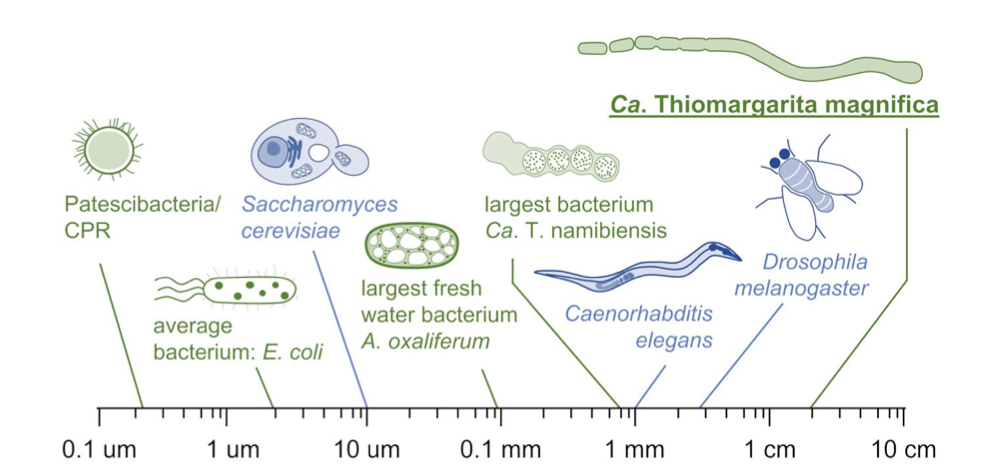
![comparison](images/short_reads/magnifica.png)
<small>[*Thiomargarita magnifica*](https://www.biorxiv.org/content/10.1101/2022.02.16.480423v1.full.pdf), [Science commentary](https://www.science.org/content/article/largest-bacterium-ever-discovered-has-unexpectedly-complex-cells)</small>

Note: By definition, microbes are supposed to be so small they can only be seen with a microscope. But a newly described bacterium living in Caribbean mangroves never got that memo. Its threadlike single cell is visible to the naked eye, growing up to 2 centimeters—as long as a peanut—and 5000 times bigger than many other microbes. What’s more, this giant has a huge genome that’s not free floating inside the cell as in other bacteria, but is instead encased in a membrane, an innovation characteristic of much more complex cells, like those in the human body.oversize bacterium is bigger than fruit flies and nematodes. that cell includes two membrane sacs, one of which contains all the cell’s DNA.

---

## Homework 
### Affine gap penalty function

$$S = O + k*E$$

```text
match = 1
mismatch = 1
gap-open = 1
gap-extend = 0.5

AC--TA
ACGTTA
```

### Email the align_sequences.py file

---

## Aligning two strings
![DP](images/fundamental_string/nw14.svg)

---

## Querying a database
![Blast](images/fundamental_string/blast.svg)

---

## Massively-parallel sequencing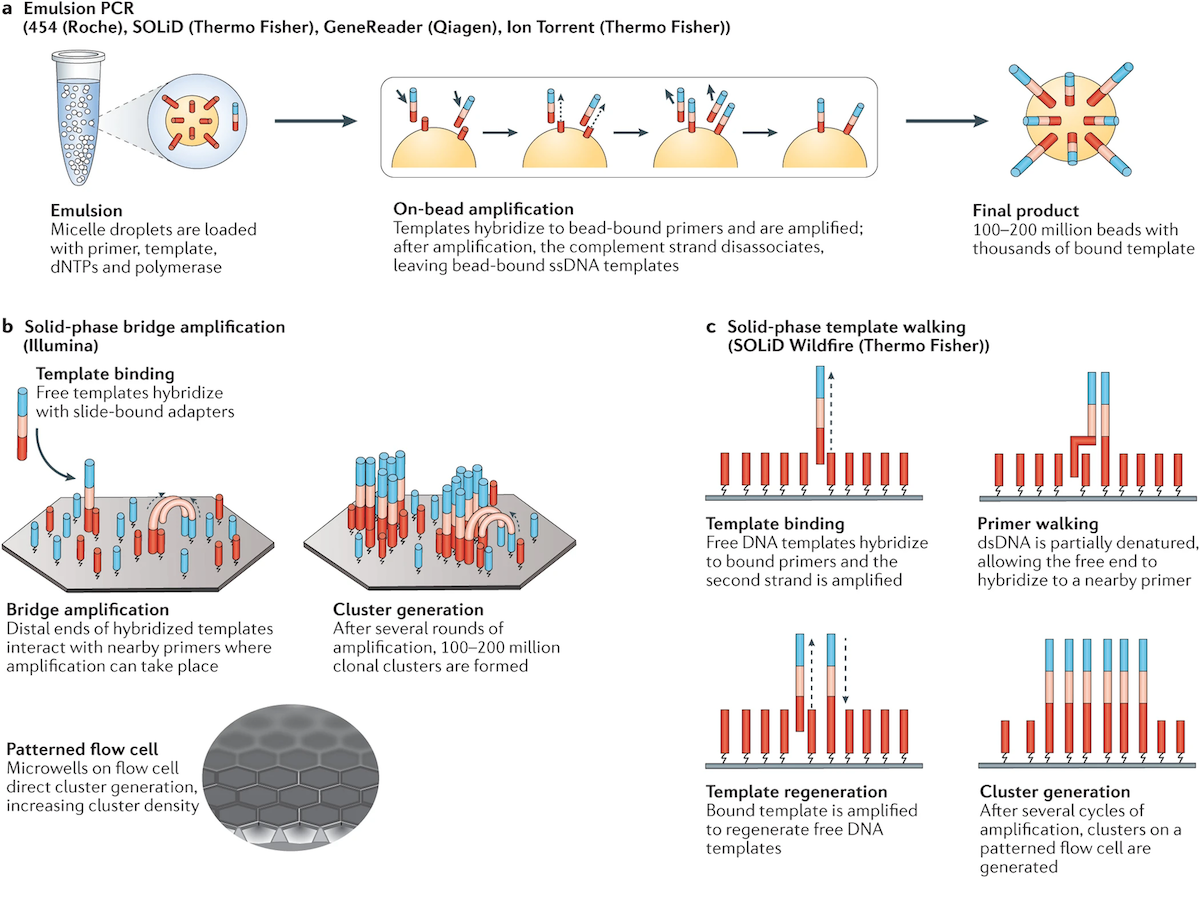
![MSP](images/short_reads/msp.png)

[PMID: 27184599](https://www.nature.com/articles/nrg.2016.49)

---

## Short-read alignment
* Input
  * Shorter sequences 
  * A sequencing run creates large number of reads 
  * Enough to cover genome multiple times
* Output
  * Position of each read $r$ of length $m$ in the reference. 
* Motivation
  * Resequencing
  * More is better!!

---

## `GATTACA` in the human genome
* Brute-force
  * Scan each *k*-mer in the reference
* Analysis:
  * Genome size: 3,000,000,000
  * Query length:  7
  * Number of comparisons: 21,000,000,000
  * Assuming each comparison takes 1/1,000,000,000 of a second
    * Running time: 0.24 days (for one 7bp read)

Note: And a possible solution is an index
 
---

## Indices
* Considerations
  * Space for the index
  * Time required to build index
  * Time required for searching
* Approaches
  * Hash-table based 
    * BFAST, MAQ, MOSIAK, SHRiMP, SOAP, $\ldots$
  * Suffix-tree or BWT based
    * Bowtie, BWA, SOAP2, $\ldots$

---

## Word position table
* Encoding : A=$00_2$, C=$01_2$, G=$10_2$, T=$11_2$
* Build an inverted index of every *k*-mer in the genome
* `GATTACA` = $10001111000100_2$ = $9156_{10}$

![word](images/short_reads/word_position.svg)

---

## Word position table
* Length $k$
  * \# of possible *k*-mers: $4^k$
* $k=7, 4^7 = 16,384$
* $k=20, 4^{20} = 1,099,511,627,776$
* $\approx$3 billion $20$-mers in genome
* Even if we build it, 99.7% of it is empty
* We don't know which cells are empty
Note: 1,099,511,627,776 impossible to store in RAM

---

![word](images/short_reads/word_position.svg)

---

![word](images/short_reads/word_position_packed.svg)

---

## Hashing
* Use a function to shrink the range
  * Map a number $n$ in $[0,R]$ to $h$ in $[0,H]$
    * $H \ll R$
    * Use 128 buckets instead of 16,384
  * $h(n) = n \\% H$
    * h(GATTACA) = $9156 \\% 128$ = 68
* Collision: multiple keys have the same hash value

---

## Hashing
* Store elements with the same key in a bucket chained together
  * good hash evenly distributes the values
* Looking up a value scans the entire bucket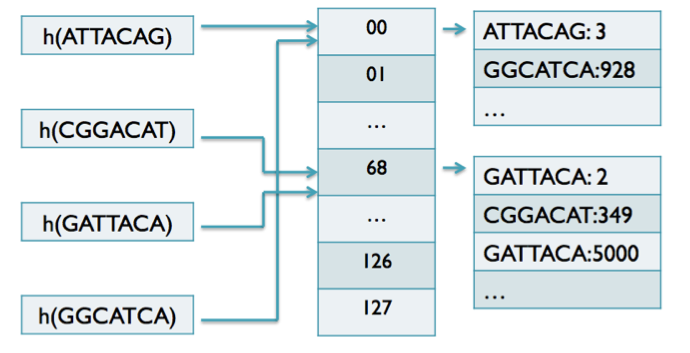

![hash](images/short_reads/hashing.png)

Note: Repetitive sequences can be a challenge both in terms of development of such data structures and analysis of runtimes. It is tricky to develop good hash functions, since we do not know the sequence at the onset. So lets take a look at some data structures that make use of some information about the sequence

---

## Tries 
* A trie is the smallest tree representing a collection of strings or keys such that
  * each edge is labeled with a character $c \in \sum$
  * for a given node, at most one child edge has label $c$, for any $c \in \sum$
  * each key is spelled out along some path starting at root
* helpful to implement *set* or *map* or *dictionary*

---

## Example of a trie
Keys: instant, internet, internal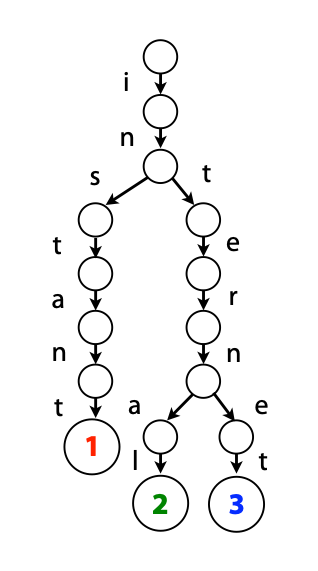

![trie](images/short_reads/trie.png)

Note: Now let us try to match "interesting", which will fail. Try matching "insta", which will fail because we did not get to a value (leaf node). Try "instant" to see how it works

---

## Tries
* Checking for presence of $P$ ($|P| = n$) traverses $\leq n$ edges
* Query time for $P$, is $O(n)$.
* Trie can represent a *k*-mer index

![trie](images/short_reads/trie_kmers.png)

Note: If we use hash tables to represent edges between node and its children. The idea of using trees is powerful as it allows a good handle on repeats. This method of building a trie will use upto 4 children at each node. Where do you start search when looking for a substring? Do we have to store aux. values?

---

## Suffix trie
* $|T| = m$
* Number of characters = $m (m + 1) / 2$

![trie](images/short_reads/suffix_trie.svg)

Note: What is the problem with this formulation? A suffix can be a prefix of another suffix.

---

## Suffix trie
* Add special terminal character $\\$$ to the end of $T$
* $ \\$ < A < C < G < T $
* Guarantees : No suffix is a prefix of any other suffix

![trie](images/short_reads/suffix_trie_term.svg)

Note: Look at aba (2nd row and 3rd row from the bottom)

---

## Suffix trie
$T = abaaba$

![suffix trie](images/short_reads/suffix_trie_example.png)

Note: Each path from root to leaf represents a suffix, and each suffix is represented by some path from root to leaf

---

## Constructing suffix trie
```code
def suffix_trie(t):
    '''Build suffix trie from t.'''
    t += '$'
    root = {}
    for i in range(len(t)):
        cur = root
        for c in t[i:]:
            if c not in cur:
                cur[c] = {}
            cur = cur[c]
    return root
```

---

## Querying a suffix trie
$T = abaaba$, $P=baa$, Is $P$ a substring of $T$?

![suffix trie](images/short_reads/suffix_trie_query.png)

Note: If we “fall off ” the trie -- i.e. there is no outgoing edge for next character of S, then S is not a substring of T. If we exhaust S without falling off, S is a substring of T. How would we check if P is a suffix? Check additionally for '$' . How would we count the number of times a string occurs as a substring in T?  Follow path labeled with S. If we fall off, answer is 0. If we end up at node n, answer equals # of leaves in subtree rooted at n.

---

## Querying a suffix trie
```code
def is_substring(st, p):
    '''Return true if p appears as a substring of t'''
    cur = st
    for c in p:
        if c not in cur:
            return False
        cur = cur[c]
    return True

```

```text
>>> st = suffix_trie('abaaba')
>>> is_substring(st, 'baa')
True
>>> is_substring(st, 'abaaba')
True
>>> is_substring(st, 'baabb')
False
```

---

## Revisiting construction
$|T| = m, m (m + 1) / 2$ chars

```code
def suffix_trie(t):
    '''Build suffix trie from t.'''
    t += '$'
    root = {}
    for i in range(len(t)):
        cur = root
        for c in t[i:]:
            if c not in cur:
                cur[c] = {}
            cur = cur[c]
    return root
```

Note: The code line 'if c not in cur' adds 1 node, and runs at most m(m+1)/2 times. In reality actual growth is closer to this worst case and increases O(m^2). Think of a^n b^n where n=2m.

---

## Suffix trie: making it smaller
Insight: Non-branching paths can be coalesced

![smaller](images/short_reads/suffix_trie_smaller.png)

---

## Suffix tree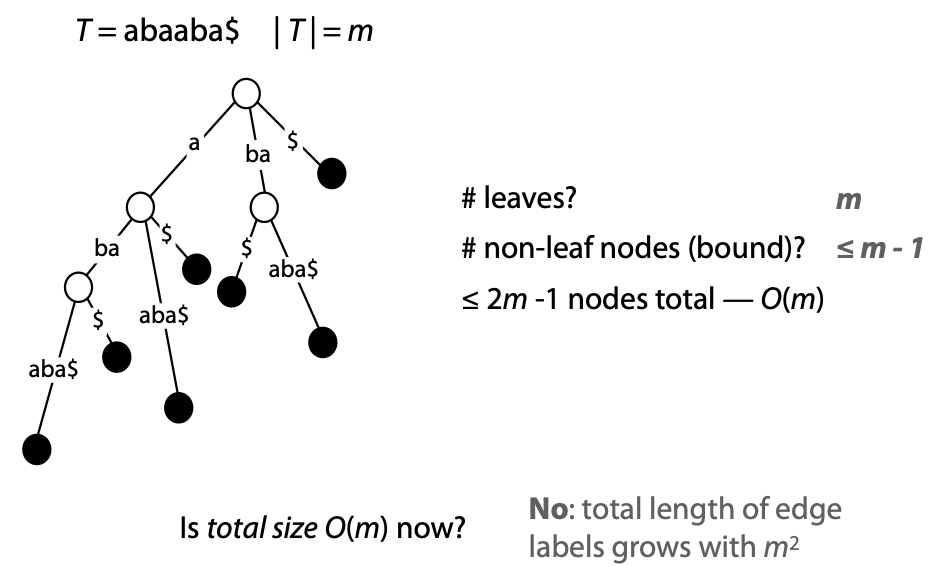
![smaller](images/short_reads/suffix_trie_smaller2.png)

Note: Now the number of nodes is O(m), but the edges are not.

---

## Suffix tree
Insight: $|T| = m$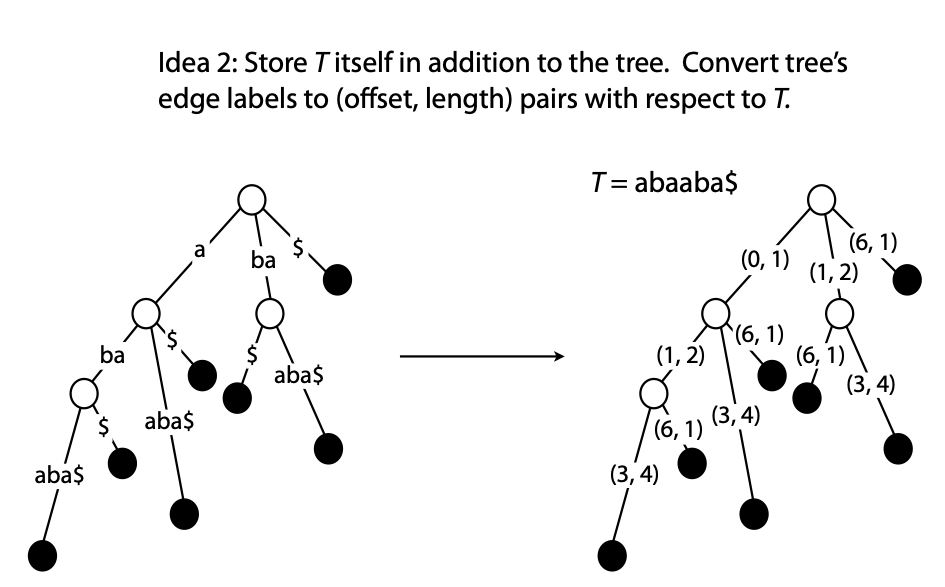

![smaller](images/short_reads/suffix_trie_smaller3.png)

Note: Space is now O(m). It was O(m^2) for the suffix trie

---

## Suffix tree
Insight: Leaves can hold offsets in $T$.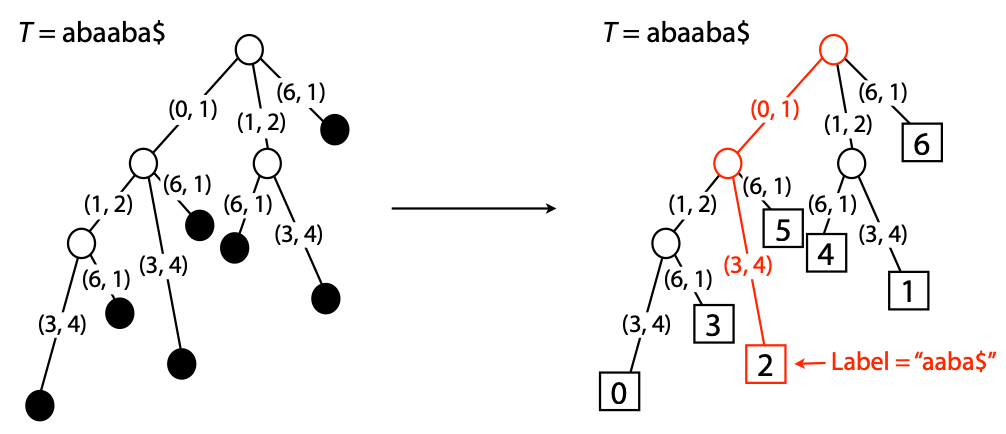

![smaller](images/short_reads/suffix_trie_smaller4.png)

---

## Constructing a suffix tree 
* Build suffix trie, coalesce non-branching paths, relabel edges
  * $O(m^2)$ time, $O(m^2)$ space
* Build single-edge tree representing longest suffix, augment to include the 2nd-longest, $\ldots$
  * $O(m^2)$ time, $O(m)$ space
* Ukkonen’s algorithm
  * O(m) time and space!
  * See the [publication](https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.74.8759&rep=rep1&type=pdf) for details.

---

## Querying a suffix tree
* Same process as for trie, but coalesced edges have to be handled.
* Suffix tree
  * $|T| = m, |P| = n, k = $ \# of occurrences
  * Does $P$ occur : $O(n)$ time
  * Report locations of $P$ : $O(n+k)$
  * Space: $O(m)$

---

## Suffix trees
* [MUMmer](https://github.com/mummer4/mummer)
* [REPuter](https://bioinformaticshome.com/tools/DNA-sequence-analysis/descriptions/REPuter.html)

* Despite the savings ($O(m)$ space), the suffix tree of human genome will be >45GB (maybe more)

---

## Suffix arrays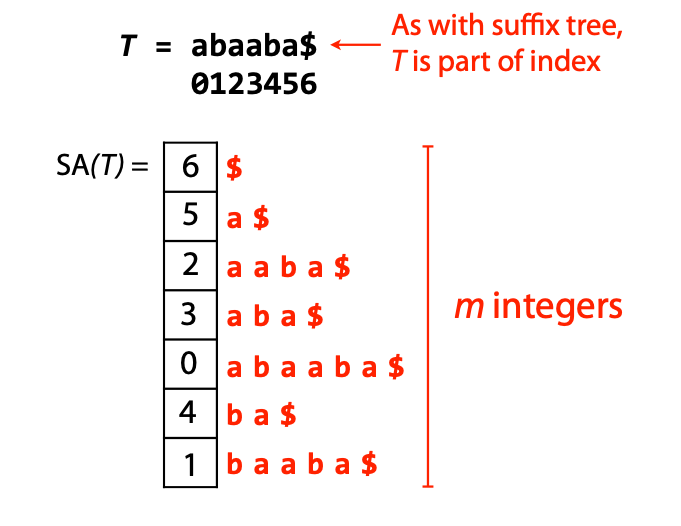
![SA](images/short_reads/SA.png)

Suffix array of $T$ is an array of integers in $[0, m)$ specifying lexicographic (alphabetical) order of $T$’s suffixes

---

## Querying a suffix array
$T = abaaba$, Is $P$ a substring of $T$?

Insights: 
* For $P$ to be a substring, it must be a prefix of $\geq$1 of $T$'s suffixes.
* Suffixes that share prefix are consecutive in the suffix array
* Do binary search to check if $P$ is a prefix of the suffix there
* $O(n~log m)$

---

## Suffix arrays 
* Query time: SA: $O(n~log m)$, Suffix tree: $O(n)$
* Index size: SA: $\approx 12 GB$, Suffix tree: $> 45 GB$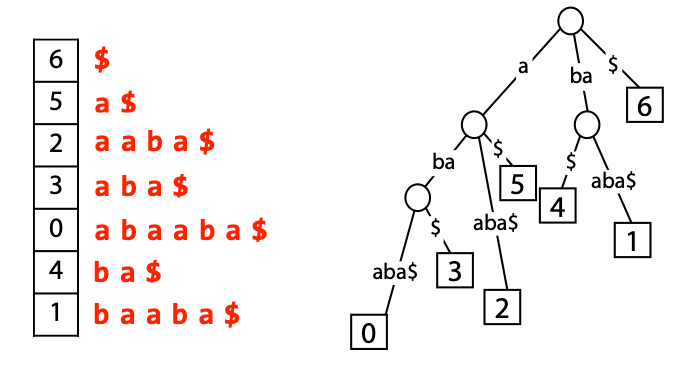

![SA_vs_ST](images/short_reads/sa_vs_st.png)

---

## Building suffix arrays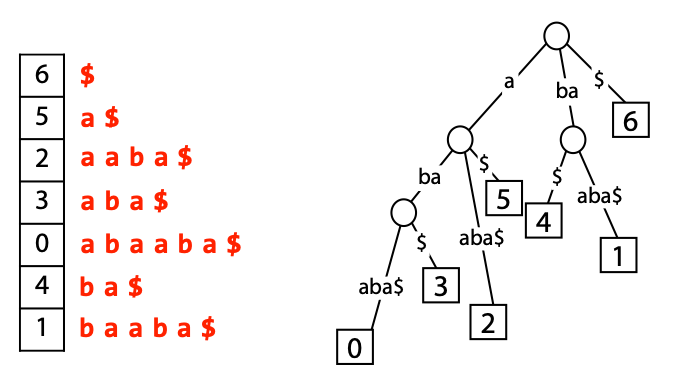
![SA_construction](images/short_reads/sa_construction.png)

* Build suffix tree
* Traverse in alphabetical order
* On reaching leaf, append suffix to array
* [Construction of suffix arrays](https://academic.oup.com/bib/article/15/2/138/212729)

---

## Burrows-Wheeler transform
* Initially developed for compression
* Reversible permutation of the characters of a string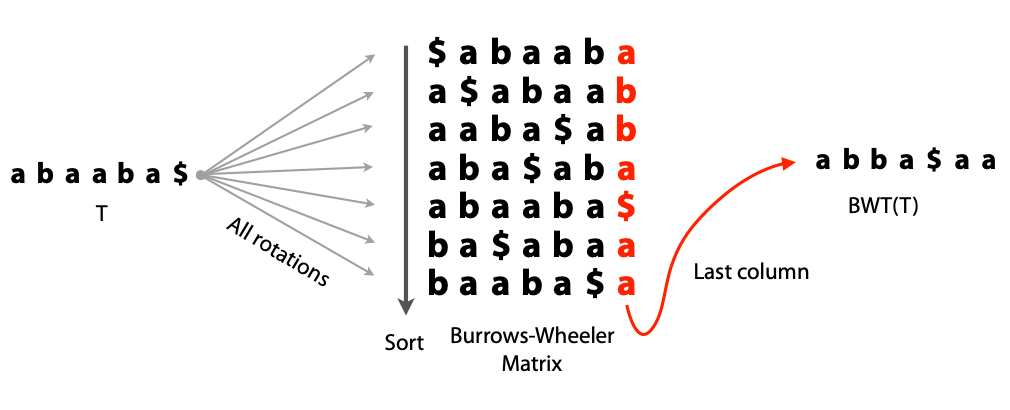

![BTW](images/short_reads/BWT.png)

---

## Burrows-Wheeler transform
```code
def rotate(sequence, n):
    return sequence[n:] + sequence[:n]

def BWT(sequence):
    seq = sequence + "$" 
    perms = [rotate(seq,i) for i in range(len(seq))] 
    return "".join([x[-1] for x in sorted(perms)])
```

```text
>>> string = "abaaba"
>>> BWT(string)
'abba$aa'

>>> string = "Let_me_tell_you_a_little_story_all_about_the_DNA"
>>> BWT(string)
'AN_$Deulyateetl___ahlmtLtlllt_ae_tybo_eu__tsioor_'
```

---

## Insight: BWT provides "structure"
$BWT(T)$ orders the characters of $T$ according to alphabetical order of their right context (characters that come after it)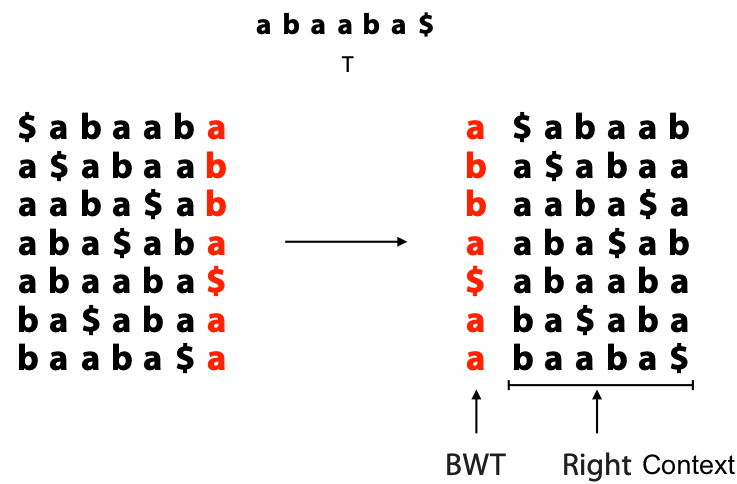

![BWT_insight](images/short_reads/BWT_insight.png)

---

## Example
![example](images/short_reads/BWT_example.png)

Burrows M, Wheeler DJ: A block sorting lossless data compression algorithm. Digital Equipment Corporation, Palo Alto, CA 1994, Technical Report 124; 1994

---

## Insight: BWT is related to suffix arrays
BWM = sort rotations of $T$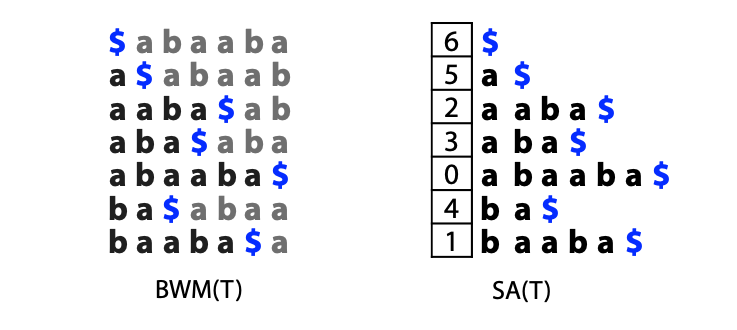

![example](images/short_reads/BWT_SA.png)

---

## BWT from SA
$BWT[i] = T[SA[i] - 1]$ if $i > 0$

![example](images/short_reads/BWT_SA.png)

---

## BWT from SA
```code
def suffix_array(T):
    """Given T, return the suffix array SA(T)."""
    suffixs = sorted([(T[i:], i) for i in range(len(T))]) 
    return map(lambda x: x[1], suffixs)

def BWT(T):
    """Given T, return the BWT(T) generated via suffix arrays."""
    T = T + "$"
    bwt = []
    for i in suffix_array(T):
        if i == 0: bwt.append('$')
        else: bwt.append(T[i-1])
    return ''.join(bwt)
```

```text
>>> string = "abaaba"
>>> BWT(string)
'abba$aa'

>>> string = "Let_me_tell_you_a_little_story_all_about_the_DNA"
>>> BWT(string)
'AN_$Deulyateetl___ahlmtLtlllt_ae_tybo_eu__tsioor_'

```

---

## Reversing the BWT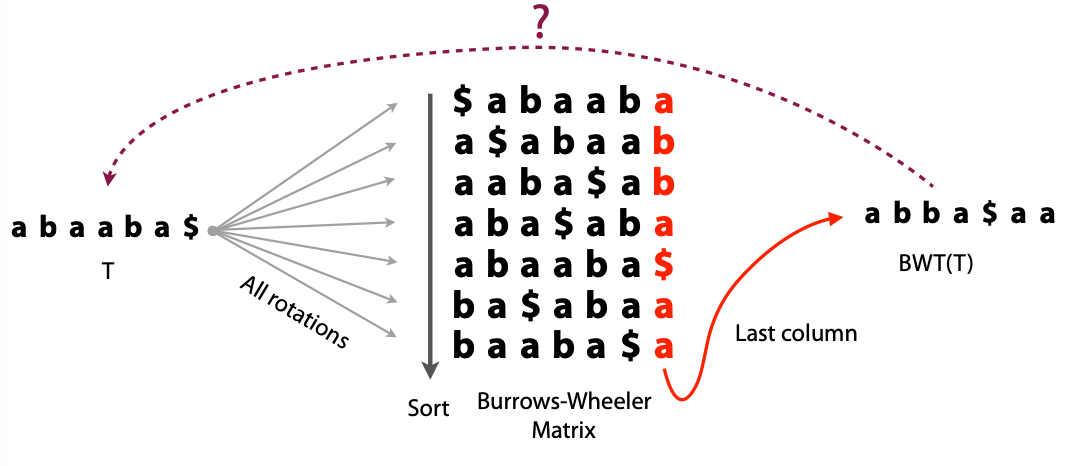
![reversing](images/short_reads/BWT_reversing.png)

---

## Reversing the BWT
![reversing](images/short_reads/inverting1.svg)
$T=abaaba$

---

## Reversing the BWT
![reversing](images/short_reads/inverting2.svg)
$T=abaaba$

---

## Reversing the BWT
![reversing](images/short_reads/inverting3.svg)
$T=abaaba$

---

## Reversing the BWT
![reversing](images/short_reads/inverting4.svg)
$T=abaaba$

---

## Reversing the BWT
![reversing](images/short_reads/inverting5.svg)
$T=abaaba$

---

## Reversing the BWT
![reversing](images/short_reads/inverting6.svg)
$T=abaaba$

---

## Reversing the BWT
```code
def invert_BWT(bw):
    '''Given BWT(T) return T.'''
    table = [""] * len(bw) 
    for i in range(len(bw)):
        table = sorted(bw[i] + table[i] for i in range(len(bw)))
    s = [x for x in table if x[-1] == '$']
    assert len(s) == 1
    return s[0][:-1]
```

```text
>>> bw = "abba$aa"
>>> invert_BWT(bw)
'abaaba'

>>> bw = "AN_$Deulyateetl___ahlmtLtlllt_ae_tybo_eu__tsioor_" 
>>> invert_BWT(string)
'Let_me_tell_you_a_little_story_all_about_the_DNA'
```

---

## Insight : LF mapping
* The $i^{th}$ occurrence of $c$ in the last column of the BWM is the same exact character as the $i^{th}$ occurrence of $c$ in the first column.

![LF](images/short_reads/LF1.png)

---

## Insight : LF mapping
* The $i^{th}$ occurrence of $c$ in the last column of the BWM is the same exact character as the $i^{th}$ occurrence of $c$ in the first column.

![LF](images/short_reads/LF2.png)

---

## FM index
* combining BWT with a few auxilliary data structures
* core of the index is $F$ and $L$ from BWM
* $L$ is the same size as $T$
* $F$ can be represented as an array of $|\sum|$ integers
* $L$ is compressible

---

## How to query?
* $P = aba$
* $T = abaaba$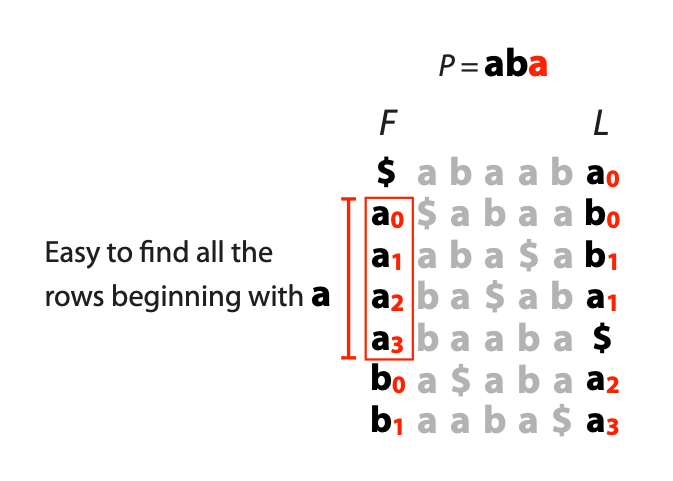

![query](images/short_reads/query1.png)

---

## How to query?
![query](images/short_reads/query2.png)

---

## How to query?
![query](images/short_reads/query3.png)

---

## How to query?
![query](images/short_reads/query4.png)

---

## How to query?
![query](images/short_reads/query5.png)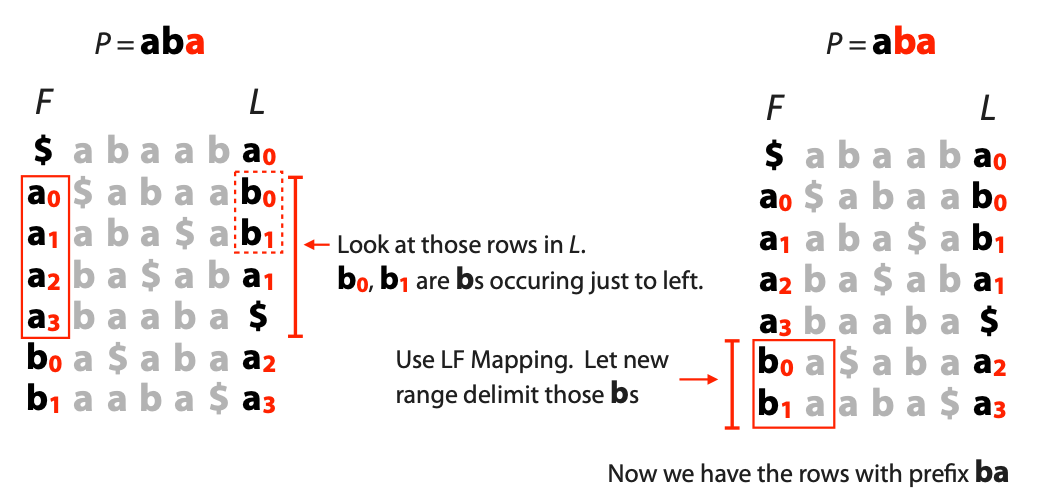

---

## How to query?
When $P$ does not occur in $T$, we eventually fail to find next character in $L$

![query](images/short_reads/query6.png)

---

## Scanning $L$ is slow
Idea : pre-calculate cumulative #a's,b's in $L$ up to every row

![query](images/short_reads/fastrank1.png)

---

## Scanning $L$ is slow
Idea : pre-calculate cumulative #a's,b's in $L$ up to every row

![query](images/short_reads/fastrank2.png)

Tally is too big ($m \times |\sum|$)

---

## Scanning $L$ is slow
Idea : pre-calculate cumulative #a's,b's in $L$ up to every $i^{th}$ row

![query](images/short_reads/fastrank3.png)

---

## Occurences in $T$
If we had suffix array, we could look up the offsets, but we do not.

![query](images/short_reads/lookup1.png)

Note: we are trying to avoid storing $m$ integers.

---

## Occurences in $T$
Again, what if we only store some SA elements?

![query](images/short_reads/lookup2.png)

---

## Occurences in $T$
Again, what if we only store some SA elements?

![query](images/short_reads/lookup3.png)

* $a$ at end of row 4 corresponds to $a$ at the beginning of row 3
* Row 3 of suffix array = 2
* Missing value in row 3 = 2 (row 3’s SA val) + 1 (# steps to row 4) = 3

---

## FM Index
$|T|=m, |P|=n$

![FM](images/short_reads/fm.png)

$O(n)$ to find occurence of $P$ in $T$

---

## FM index 
Components of index

* $F : |\sum| integers$
* $L : m$ characters
* $SA$ samples: $m . a$ integers
* Checkpoints: $n . |\sum| . b$ integers

Assuming 2 bits per nucleotide, T=human genome, a = 1/32, b = 1/128, the total size comes to 1.5 GB

Note:_a is the fraction of SA elements kept, b is the fraction of tallies kept

---

## Suffix index bounds
![bounds](images/short_reads/bounds.png)

---